Lyapunov Exponents of a Forced Logistic map
See the September 1991 issue of Scientific American
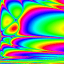
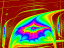
The Fractal Rabbit Lyapunov Wing of the Savage Rabbit Art Gallery proudly presents these creations by Savage Rabbit Artists and SCO employees Ronald Joe Record and Andrew Sharpe. These fantastic creations represents the Lyapunov exponents of a forced oscillator modelled by parameterizing the logistic map. The Lyapunov exponent(s) of a dynamical system can be used to numerically characterize the qualitative behaviour of the system. A positive Lyapunov exponent is indicative of rapidly diverging orbits or "sensitive dependence on initial conditions". This is one characteristic of "chaos".
Colors represent the behaviour of the model ranging from stable periodic or fixed orbits to chaotic or "strange" attractors. The color figure graphically divides parameter space into stable and chaotic regions.
The first room of this wing has the following images available for viewing
Click on the Desired Image
You can select one of the images above for viewing, Continue to the Next Room of this wing, Skip to the Third Room of this wing, or enter the Endomorphic Rabbit Wing, visit the Mandelbrot Rabbit Wing, check out the Topographic Rabbit Wing, saunter through the Sporographic Rabbit Wing, zip over to the Iterographic Rabbit Wing, or stand at the Main Entrance to the Fractal Wing.
Or, you may wish to walk over to the Astro Rabbit Wing, enter the Pop Savage Art Wing, visit the Self Savage Portrait Wing, or stand at the Main Entrance to the Art Gallery
This HTML document and this wing of the Savage Rabbit Art Gallery maintained by
Ron Record (rr@ronrecord.com) x7604







 Return to Welcome Home Page
Return to Welcome Home Page